其实这节就是换成 Allen-Cahn 方程,然后多个变量而已,主要是俺不想实现 Voronoi 结构(逃
简介
上一部分我们以调幅分解为基础讨论了浓度场在 Cahn-Hilliard 方程下的演化过程。对相场方法而言,另一个无法绕开的演化方程则是针对非保守场变量的 Allen-Cahn 方程。这一部分我们将对晶粒长大过程进行分析,了解 Allen-Cahn 方程并使用它进行晶粒长大过程的模拟。
晶粒长大
晶粒长大的过程各位材料学子应该已经很熟悉了,在这个过程中,由于晶界能量较高而体自由能相较之下较低,体系能量希望能够达到全局最低的情况下,需要尽可能地降低晶界能在总能中的占比,提高体自由能的占比。但是,晶界能的能量密度应该是某个变化不大的数值,几乎可以看作定值,因此为了降低晶界能,体系会倾向于降低晶界的体积,提高晶体的体积。这样一来,从宏观上的表现来看就是晶粒长大的过程。
这样来看,晶粒长大过程对能量的需求是:晶粒内的能量较低,晶界处的能量较高。那么,之前的 Cahn-Hilliard 方程 + 浓度的组合是否可行呢?我们需要考察晶粒长大过程中涉及什么量。由于同一种相的不同的晶粒都具有相同的成分,故无法用浓度来表示某一个特定的晶粒;不考虑取向的话,晶粒与晶粒之间只存在位置,大小之间的差异,也就是单纯的几何差异。而在界面上,一个晶粒与另一个晶粒相接,还需要某种方法来表示某些晶粒之间的界面。而且在晶粒生长的过程中,小晶粒可能会变得更小最后消失。
综合上面来看,Cahn-Hilliard 方程和浓度并不适合这个问题,那么应该如何处理呢?相场方法中我们经常使用场变量来表示某个区域存在某种性质,那么可以考虑为每个不同的晶粒赋予一个不同的变量,比如假设有 10 个小晶粒,那么就使用 10 个变量来分别代表这些晶粒区域。其次,考虑到这些晶粒仅存在位置上的差异,我们需要在他们参与热力学讨论时没有数值上的差异。我们可以让这些变量类比于浓度:存在于某区域时变量为 1,不存在则变量为 0。这样,界面部分也可以简单地表示出来:所有序参量都不为 0 的部分即为界面部分,这样也摆脱了追踪界面的麻烦。
那么,我们需要使用什么样的方程来演化这样的场呢?这个场,根据上面的分析,是不满足守恒条件的。我们这里就不卖关子了(因为上个部分已经剧透了),答案就是使用 Allen-Cahn 方程。那么这个体系的能量呢?这个方程要怎么理解呢?
模型分析
演化方程
我们先看看 Allen-Cahn 方程吧:
$$ \frac{\partial \eta_i}{\partial t} = -L_{ij}\frac{\delta F}{\delta \eta_j} $$简单地令人发指(也许)。简单来说,就是某个变量的变化速率受到所有的势的加权求和影响。但是要如何理解这个公式呢?它是怎么来的呢?其实如果有看过上一篇内容的话,应该已经猜到了。如果物质不守恒,那么物质流的散度项就可以替换成某种别的形式。这个所谓“别的形式”需要满足这些条件:
- 需要和能量/势相关以满足热力学要求
- 最终是令体系演化达到平衡的
那么干脆就让演化速率和势成正比好了,然后用符号调整演化方向最终是朝着体系稳定的方向发展的。这样就得到了上面的 Allen-Cahn 方程。
除了这样解释之外,我们还可以采用更加数学一些的方式。当我们需要体系朝着稳定方向发展时,实际上也就是说我们希望体系自由能向着最小的方向发展。而当体系稳定时,我们有如下关系:
$$ \frac{\delta F}{\delta \eta_i} = 0 $$这里需要运用我们已经了解到的泛函导数的相关内容,当泛函导数为 0 时,说明这个构型的 $\eta_i$ 是令泛函 $F$ 取得极值的点。考虑到 $F$ 具有能量的物理意义,这里的极值自然是极小值。在热力学中,极小值表示体系至少出于亚稳态。当该构型下恰好能量是最低的时,则体系出于热力学稳定状态。
这样一来,体系的稳态表示就没有任何问题,但是我们需要的是向着稳态演化,而不是直接求得稳态的状态。这时就需要使用经典的数值方法:弛豫法。我们给方程右边的 0 改变为某个微小变量。这个变量的意义是令体系向着平衡态发展,所以这个变量应该越来越小。通过不断迭代,最终这个微小变量将趋近于 0,此时我们便得到了平衡稳态的结果。那么这个微小变量,按照我们的预想,应该和场变量本身是相关的;不断迭代的过程又说明和时间相关。要让这个微小变量不断减小,根据能量函数(泛函)的特性,干脆就让弛豫变量设置为场变量的演化速率,再乘上一个弛豫常数。由于演化方向,弛豫常数应该是一个小于 0 的值,最后考虑所有项的影响,就得到了这个方程。
最后要指出,上面这些都是从一些不够物理的,十分唯象的角度来提出的。实际上,Allen-Cahn 方程是建立晶界迁移速率与驱动力成正比这一结论得出的,而这一结论更是从晶体排列构型的基态得到的。
关于 A-C 方程的一些碎碎念
另外,这个形式的方程非常常见,或者说,水非常深。几乎可以在物理学的许多领域见到这个方程,而对这个方程的描述都各有千秋。有人称其为 Landau–Khalatnikov 方程(描述磁性),有人称之为 Model A(界面动力学,[Theory of dynamic critical phenomena](https://doi.org/10.1103/RevModPhys.49.435)),还有一些奇奇怪怪的名称,但是这些文章几乎都没有对这个方程做出详细的解释。也许这些方程是从某些物理直觉中得到的?又或者这些这些方程有其更深刻的数学/物理背景,但是这些我也无从得知。能量构造
本模拟使用的能量模型来自D. Fan 与 LQ. Chen 的文章,其构造如下:
$$ \begin{align*} F &= \int_\omega f_{bulk} + f_{int} \,\mathrm{d}\Omega;\\ f_{bulk}\left(\eta_0,\eta_1,\cdots,\eta_N\right) &= \sum_{i}^{N}\left( -\frac{A}{2}\eta_i^2 + \frac{B}{4}\eta_i^4 \right) + \sum_{i}^{N}\sum_{j\neq{}i}^{N}\eta_i^2\eta_j^2;\\ f_{int}\left(\nabla\eta_0,\nabla\eta_1,\cdots,\nabla\eta_N\right) &= \sum_{i}^{N}\frac{\kappa_i}{2} \left| \nabla \eta_i \right|^2. \end{align*} $$其中的界面能项我们不再赘述,因为它就是上一部分介绍过的能量而已,只不过这里要加上所有序参量的贡献而已。我们重点放在体能上。和上次相比,体能的部分变化很大,但是也有一些熟悉的部分。我们把这个体能重新整理一下:
$$ \begin{align} f_{bulk}&= \sum_{i}^{N}\left( -\frac{A}{2}\eta_i^2 + \frac{B}{4}\eta_i^4 \right) + \sum_{i}^{N}\sum_{j\neq{}i}^{N}\eta_i^2\eta_j^2\\ &=\sum_{i}^{N}\left( -\frac{A}{2}\eta_i^2 + \frac{B}{4}\eta_i^4 \right) + \sum_{i}^{N}\eta_i^2 \sum_{j\neq{}i}^{N} \eta_j^2\\ &=\sum_{i}^{N}\left(\left( -\frac{A}{2}\eta_i^2 + \frac{B}{4}\eta_i^4 \right) + \eta_i^2 \sum_{j\neq{}i}^{N} \eta_j^2\right)\\ &=\sum_{i}^{N}\left( \left(-\frac{A}{2} + \sum_{j\neq{}i}^{N} \eta_j^2\right) \eta_i^2 + \frac{B}{4}\eta_i^4 \right)\\ \end{align} $$上面第二个等号是由于对 $j (j\neq i)$ 的求和的部分与 $i$ 无关,我们可以把 $\eta_i^2$ 从二重求和中提出来, 然后第三个等号中把对 $i$ 的求和的部分提取合并,最后第四个等号里提出 $\eta_i^2$,把 $\sum_{j\neq{}i}^{N} \eta_j^2$ 作为系数和 $-\dfrac{A}{2}$ 合并。现在我们把目光放在求和里面的这个,关于 $\eta_i$ 的多项式。为简单起见,我们设 $A = B = 1$。下面是这个函数在 $\sum_{j\neq{}i}^{N} \eta_j^2 = 0$ 时候, 即 方程(1) 的第一项的图像(当然,这个假设不够合理,但是我们可以先看看)。
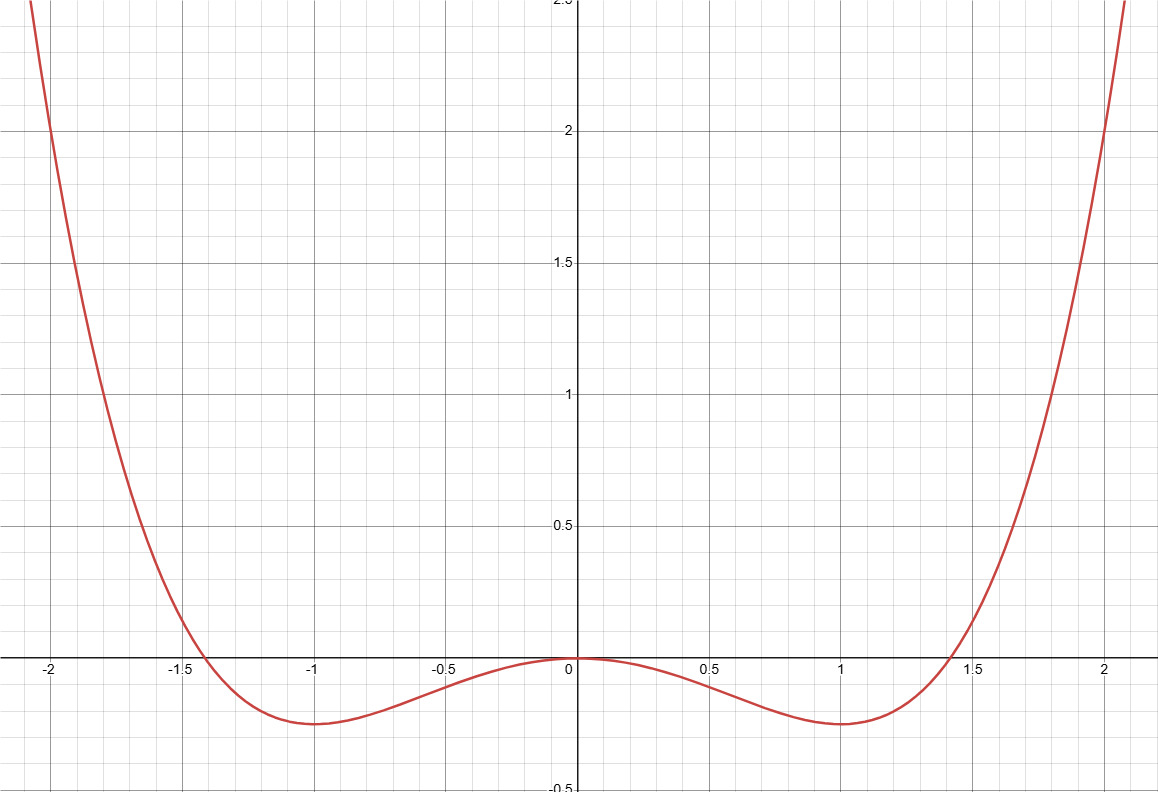
是我们很熟系的双势阱,但是这里有一些问题:序参量实际上不能小于0,也不应该大于1。如果我们只关注 0 到 1 之间的值,不难发现现在这个能量的最低点处在 $\eta = 1$ 的地方。这很合理:在其余的所有序参量(我们简称所有的 j ,对应的本个序参量则为 i)都为 0 的情况下,或者说在没有任何 j 的点,i 占据该点是理所应当的。考虑到每个序参量都是平权的,这说明了这个方程是符合体相内部的热力学要求的。接下来我们考察当这个求和项不为 0 的情况。j 求和的值的变化范围我们先设为 0 到 2。
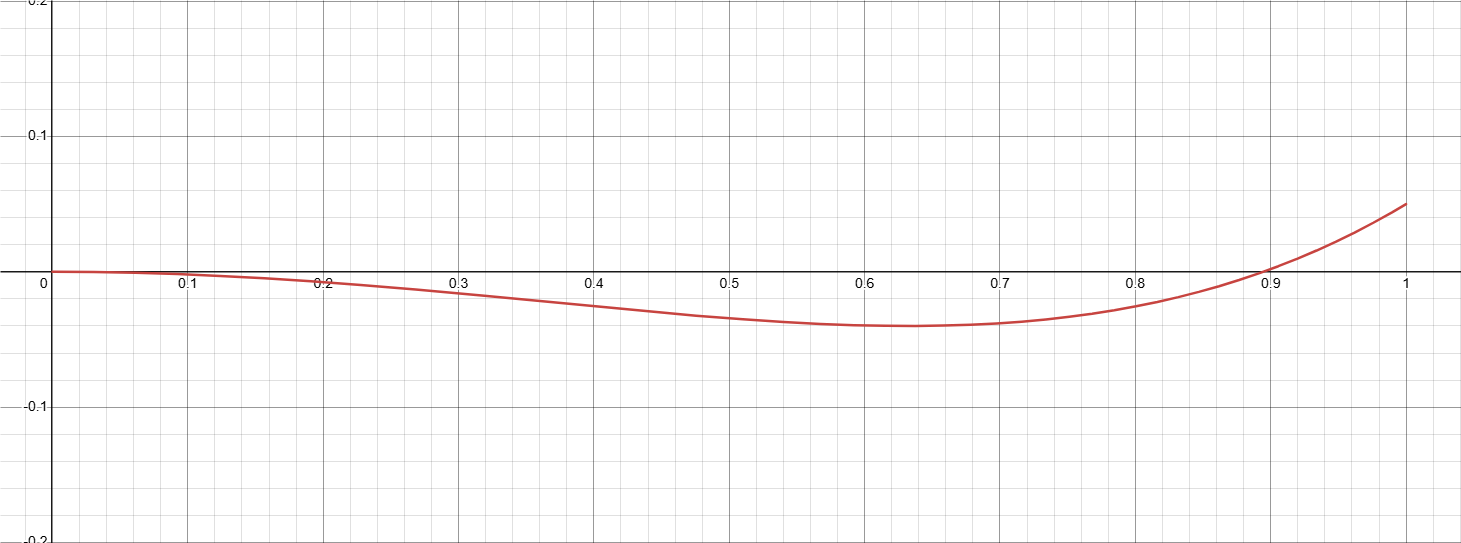
可以看到,当 j 不为 0 时,结果也是合理的,这里 i 的值也不在 1 处取到最小值,而是在 0 到 1 之间的区域取到最小值了。感兴趣的话您可以自行尝试绘制这里的图像,然后调整这些值,观察序参量-能量曲线的最低点位置。当然,我们也可以使用更数学一些的方式来研究这里的最低点取值情况,不过图像方法更加直观一些就是了。最后来简单描述一下表达式 (1) 的物理意义:将每个参量都赋予一个类势阱的能量,然后通过第二项的交叉作用将这些能量结合在一起。第二项的二重和即是其他参量对本参量的影响。
相场演化方程与扩散方程之间的关系
我们其实很早就发现了 Allen-Cahn 和 Cahn-Hilliard 两个方程与扩散方程(Fick 定律)之间的相似性。我们现在来更仔细地看看这些方程与 Fick 定律之间有什么关系吧。
对于 Cahn-Hilliard 方程而言,可以看到它与 Fick 第二定律的形式非常地像。如何看待这种相似性呢?我们可以讲,对于 Fick 第二定律而言,其提供扩散驱动力的部分是浓度本身,或者说浓度的梯度。而当这个驱动力放在更加广阔的语境下时,例如,上坡扩散等现象发生时,我们必须根据热力学原理,使用扩散势来解释这类现象。因此,可以将 Cahn-Hilliard 方程看作是更加符合热力学原理的扩散方程。
那么,Allen-Cahn 方程呢? 我们需要把 Allen-Cahn 方程和经典的能量泛函构造联系起来,并展开公式。这时我们得到:
$$ \frac{\partial \eta_i}{\partial t} = L_{ij}\nabla^2 \eta_j - L\mu_i $$这个形式,熟悉吗?如果去掉第二项,那么这个方程就是 Fick 第二定律!那么第二项代表了什么呢?第二项实际上代表了某种界面上发生的反应。为什么说是界面上的?观察这个方程与 Fick 第二定律所代表的情况,第一项代表了某个变量是守恒的,然而第二项的化学势的存在打破了这种平衡。我们使用界面上的反应来解释这种情况的出现是最合适的:不守恒的序参量是被“消耗”掉了。实际上,按照这种思路,我们可以构造出更加复杂的演化方程,即根据体系内存在的反应,向能量中添加反应造成的能量变动,最后则会反映到 Allen-Cahn 方程的反应项中。
问题分析
OK,现在我们应该对这次模拟所需要的演化方程以及能量构造有一定的理解了。这次我们要尝试的问题是:假设有两块单晶,一块出于另一块的中心,中心晶粒的形状是半径 14 单元的一个圆盘。现在需要通过模拟得到晶粒长大的过程。
十分简单的问题,只需要创建两个序参量网格,然后对每个网格进行迭代即可。也许求和部分有一些问题,然而可以通过一些程序技巧简化一部分的运算。直接看代码吧。
代码实现
我们依旧使用 C++ 实现,这里一次性全都贴出来。
1#include <filesystem>
2#include <fstream>
3#include <iostream>
4#include <string>
5#include <vector>
6
7double laplacian(double eta_l, double eta_r, double eta_d, double eta_u, double eta_c, double dx) {
8 return (eta_l + eta_r + eta_d + eta_u - 4.0 * eta_c) / (dx * dx);
9}
10
11double df_deta(double A, double B, double eta_square_sum, double this_eta) {
12 return -1.0 * A * this_eta + B * this_eta * this_eta * this_eta + 2.0 * this_eta * (eta_square_sum - this_eta * this_eta);
13}
14
15std::ofstream create_vtk(std::string file_path, int time_step) {
16 std::filesystem::create_directory(file_path);
17 std::filesystem::path f_name{"step_" + std::to_string(time_step) + ".vtk"};
18 f_name = file_path / f_name;
19
20 std::ofstream ofs{f_name};
21 return ofs;
22}
23
24void write_vtk_head(std::ofstream &ofs, std::string filename, double dx, size_t Nx, size_t Ny) {
25 ofs << "# vtk DataFile Version 3.0\n";
26 ofs << filename << std::endl;
27 ofs << "ASCII\n";
28 ofs << "DATASET STRUCTURED_GRID\n";
29
30 ofs << "DIMENSIONS " << Nx << " " << Ny << " " << 1 << "\n";
31 ofs << "POINTS " << Nx * Ny * 1 << " float\n";
32
33 for (size_t i = 0; i < Nx; i++) {
34 for (size_t j = 0; j < Ny; j++) {
35 ofs << (double)i * dx << " " << (double)j * dx << " " << 1 << std::endl;
36 }
37 }
38 ofs << "POINT_DATA " << Nx * Ny * 1 << std::endl;
39}
40
41void write_vtk_data(std::vector<std::vector<double>> mesh, std::ofstream &ofs, std::string data_label, double dx) {
42 size_t Nx{mesh.size()}, Ny{mesh.at(0).size()};
43 ofs << "SCALARS " << data_label << " float 1\n";
44 ofs << "LOOKUP_TABLE default\n";
45 for (size_t i = 0; i < Nx; i++) {
46 for (size_t j = 0; j < Ny; j++) {
47 ofs << mesh.at(i).at(j) << std::endl;
48 }
49 }
50}
51
52int main() {
53 int Nx = 64;
54 double dx = 0.5, dt = 0.005;
55 int nstep = 20000, pstep = 100;
56 int radius = 14;
57 double mobility = 5.0, kappa = 0.1;
58 double A = 1.0, B = 1.0;
59 double eta_trun = 1e-6;
60
61 std::vector<std::vector<double>> grain_1(Nx, std::vector<double>(Nx, 0));
62 auto grain_2 = grain_1;
63
64 for (int i = 0; i < Nx; i++) {
65 for (int j = 0; j < Nx; j++) {
66 if ((i - Nx / 2) * (i - Nx / 2) + (j - Nx / 2) * (j - Nx / 2) < radius * radius) {
67 grain_1.at(i).at(j) = 1.0;
68 grain_2.at(i).at(j) = 0.0;
69 } else {
70 grain_1.at(i).at(j) = 0.0;
71 grain_2.at(i).at(j) = 1.0;
72 }
73 }
74 }
75
76 std::vector<std::vector<std::vector<double>>> grains = {grain_1, grain_2};
77 auto grains_temp = grains;
78
79 for (int istep = 0; istep < nstep + 1; istep++) {
80 std::vector<std::vector<double>> grain_square_sum(Nx, std::vector<double>(Nx, 0));
81 for (int igrain = 0; igrain < 2; igrain++) {
82 for (int i = 0; i < Nx; i++) {
83 for (int j = 0; j < Nx; j++) {
84 grain_square_sum.at(i).at(j) += grains.at(igrain).at(i).at(j) * grains.at(igrain).at(i).at(j);
85 }
86 }
87 }
88 for (int igrain = 0; igrain < 2; igrain++) {
89 for (int i = 0; i < Nx; i++) {
90 for (int j = 0; j < Nx; j++) {
91 int im = i - 1, jm = j - 1, ip = i + 1, jp = j + 1;
92 if (im == -1) {
93 im = Nx - 1;
94 }
95 if (jm == -1) {
96 jm = Nx - 1;
97 }
98 if (ip == Nx) {
99 ip = 0;
100 }
101 if (jp == Nx) {
102 jp = 0;
103 }
104 double eta_l = grains.at(igrain).at(im).at(j);
105 double eta_r = grains.at(igrain).at(ip).at(j);
106 double eta_d = grains.at(igrain).at(i).at(jm);
107 double eta_u = grains.at(igrain).at(i).at(jp);
108 double eta_c = grains.at(igrain).at(i).at(j);
109
110 grains_temp.at(igrain).at(i).at(j) = eta_c - mobility * dt * (df_deta(A, B, grain_square_sum.at(i).at(j), eta_c) - kappa * laplacian(eta_l, eta_r, eta_d, eta_u, eta_c, dx));
111
112 if (grains_temp.at(igrain).at(i).at(j) > 1.0 - eta_trun) {
113 grains_temp.at(igrain).at(i).at(j) = 1.0;
114 }
115 if (grains_temp.at(igrain).at(i).at(j) < eta_trun) {
116 grains_temp.at(igrain).at(i).at(j) = 0.0;
117 }
118 }
119 }
120 }
121 grains = grains_temp;
122 if (istep % pstep == 0) {
123 auto ofs = create_vtk("./result", istep);
124 write_vtk_head(ofs, "step_" + std::to_string(istep), dx, Nx, Nx);
125 write_vtk_data(grains.at(0), ofs, "grain_1", dx);
126 write_vtk_data(grains.at(1), ofs, "grain_2", dx);
127 }
128 }
129}
这次我们优化了 vtk 文件的生成函数,使之能够分部写入。其余部分都是非常简单的。考虑到计算过程,这次的模拟甚至比上次的还要简单一些。运行这里的代码之后,程序会在其位置生成一个 result/ 文件夹并且把结果文件都放在里面。和之前一样,使用 Paraview 即可打开这些文件了。
结果
和上次一样,这里就贴一下几张截图。
 |  |
| 第5步 | 第25步 |
 |  |
| 第75步 | 第150步 |
可以看到,随着时间推进,小晶粒(中间红色部分)被大晶粒(蓝色部分)不断吞并。而且根据步数,可以看到一开始由于两个晶粒的体积近似,演化速率并不大;随着不断的演化,两个晶粒的体积差距越来越大,演化速率也变大了。这符合我们对晶粒长大过程的认知,小晶粒会非常快速地消失,而较大的晶粒则会演化地比较慢。
结语
我刚开始写的时候也没有想到这里会写这么多的模型解析的内容。不过也算是补充了之前对相场模型介绍不足的问题吧。这里的模拟部分,因为是参考的 Programming Phase Field Modeling 的 Case Study II,实际上还应该实现一下 Voronoi 结构的模拟,然后把多序参量情况下的代码结构处理一下。这里的代码应该是没有完全支持多相场情况的。但,我实在不想手搓一个 Voronoi 结构生成的函数,而能生成这个结构的库都太大了,我也不想给这个示例/教学代码引入什么第三方库。所以,结果就是,这里只实现了两个晶粒的模拟。也许之后会突然对 Voronoi 结构生成算法开窍了,然后就写进这个程序里呢?那也是以后的事了。
和上一个部分一样,对模型和模拟过程更深层的理解是离不开调整参数进行测试的。这两个案例都是比较简单的案例,可调的参数并不多,而且在模拟一开始的时候就已经有了参考的参数了,也不是面对的实际存在的体系,填入的数字的物理意义并没有很大,或者说是比较唯结果论的一些数据。在面对实际物理体系的时候,填参数这块儿是模拟过程最折磨的部分了。如何精确地控制这些参数,让他们配合起来形成一个符合物理特性,而且也能跑出合理结果,这也许是相场方法最麻烦的点。参数的可解释性经常会和参数的数值特性相悖,而能平衡二者的结果几乎都是经过精心设计的。总而言之,多调参数总没错。
那么这就是这个教程(自称)系列的最后一部分了。相场方法作为一种材料模拟方法,能做的东西非常多,但是其本身也有一定的限制。它最大的限制就是所谓的扩散界面,这样的界面解决了微分方程不好解的问题,但是也让这个方法很容易滑向物理意义不明确的道路,也经常会因为界面的存在而导致一些模拟发生数值失稳(即便引入界面常常就是希望能解决数值失稳的)。这些特点注定让相场成为一门比较复杂的交叉学科:需要对材料科学有深入的理解,对材料的物理特性有清晰的物理图像,对数值方法有清晰的认知,明白各种方法之间的优缺点选择合适的方法,最后还需要有一定的程序能力来支撑实现模拟。这也许也是相场复杂的地方吧。
相场方法并不是一个很新的模拟方法,但是它还有很大的发展空间。不论是比较传统的调幅分解的深入研究模拟,还是使用相场法研究固体力学、电磁学、流体力学这些更复杂的外场,又或者是开发新的程序软件来帮助进行相场模拟,甚至是使用机器学习来辅佐相场计算,这些都是相场正在发展的方向。这个系列的教程希望能够提供相场方法最基础的部分,比如相场的数学基础,程序基础等等。这些内容应该能够成为学习相场过程中比较重要的工具,以便于学习和发展更深层的更复杂的理论/实践。希望阅读本教程的您可以从中有所收获。
那么就是这样,最后祝您生活愉快,科研顺利~
